Fortran vs. Python

Source

A colleague of mine wrote a few lines of code which simulate a longitudinal x-ray scan of a periodic heterostructure in the kinematical approximation. Gaussian fluctuations in the vertical position of the layers are explicitely included. Since MadMax doesn't offer this possibility, I got very interested in this little simulation.

Here's the Fortran code:

program kinemat
implicit none
integer Nat1,Nat2,Nperiods,i,j,n,Nbuffer
integer, parameter :: Np=50000
real pi,a,q,eps,t1,t2,t,a1,a2,sigma,R,Tbuffer
complex Ffilm,Fbuffer,FonePeriod,Fperiodic
complex, parameter :: Im=(0.,1.)
pi=4.*atan(1.)
a=0.2593 ! spacing [nm]
Nat1=3./a ; Nat2=14./a ; Nbuffer=500./a
Nperiods=4
eps=0.02
sigma=0.
a1=(1.+eps)*a ; a2=a
t1=Nat1*a1 ; t2=Nat2*a2 ; t=t1+t2 ; Tbuffer=Nbuffer*a2
open (10,file='kinemat.dat')
do i=1,Np
    q=2.*pi/a + 3.*(-1.+2.*i/Np)
    R=exp(- (q-2.*pi/a)**2*sigma**2/2.)
    FonePeriod=( (exp(Im*q*t1)-1)/(exp(Im*q*a1)-1) + &
   (exp(Im*q*t2)-1)/(exp(Im*q*a2)-1)*exp(Im*q*t1) )
    Fperiodic=(exp(Im*q*t*Nperiods)-1)/(exp(Im*q*t)-1)
    Ffilm=exp(Im*q*Tbuffer)*Fperiodic*FonePeriod*R
    Fbuffer=(exp(Im*q*Tbuffer)*R-1.)/(exp(Im*q*a2)-1.)
    write (10,*) q,log(abs(Ffilm+Fbuffer)**2)
enddo
end program kinemat

For such a small task, Fortran is perhaps not the ideal choice, and I thus decided to "port" the code to Python. What I initially didn't understand was the "clumsy" way to define the thicknesses. If t2 = nat2*a2, and nat2 = 14/a with a = a2, then t2 = 14. Right?

Right. But what happens when you apply the same to t1 and nat1? I thought it'd be basically the same, but what I didn't see and understand (blind as a mole, dumb as a pole) is that nat1 and nat2 are defined as integers in the above code. Fortran then automatically rounds these numbers ... and that's essential! Look at the following expression, which is the basic element of the equations above:

$\Large{ \frac{e^{inq} - 1}{e^{iq} - 1}}$

With an integer $n$ and at $q = 2 \pi$, this expression is indeterminate. This single value is simply ignored by all implementations, be it in Fortran, Python, or Mathematica. However, if n is not an integer, the ultimate mathematical sin is commited: divison by 0. OMG! 😄

Just enter the following lines into an ipython console and see for yourself:

q = arange(-2.5*pi,2.5*pi,0.0001)
int=(exp(1j*10*q)-1)/(exp(1j*q)-1)
plot(q,int)

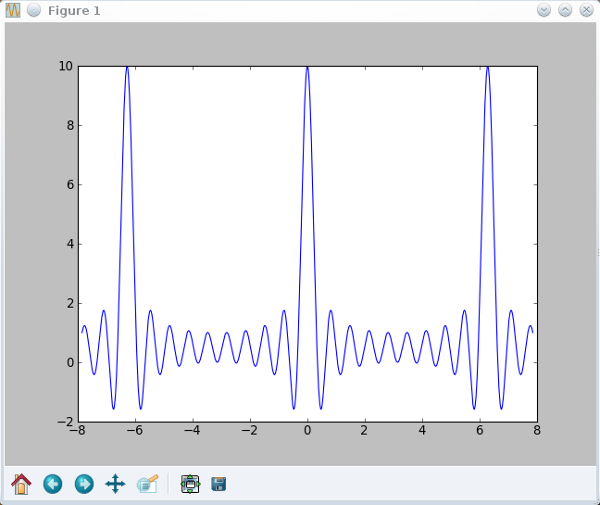
Nice and well behaving. In contrast:

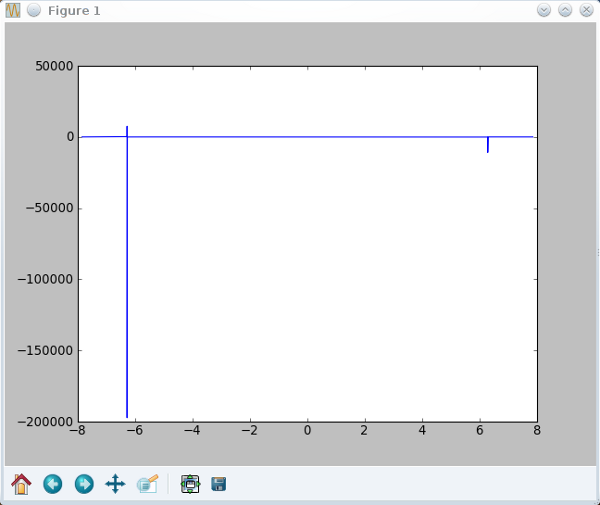
int=(exp(1j*10.371*q)-1)/(exp(1j*q)-1)

Horrible *shudder*

Here's the final python code:

#!/usr/bin/python
# -*- coding: utf-8 -*-
from scipy import *
from pylab import *
c = 0.51846/2
eps = 0.02
cqw = (1+eps)*c
cb = c
nqw = floor(3/c)
nb = floor(14/c)
nbuffer = floor(500/c)
tqw = nqw*cqw
tb = nb*cb
t = tqw + tb
tbuffer = nbuffer*c
nperiods = 4
sigma = 0
i = arange(-3,3,0.0001)
    q = 2*pi/c+i
    R = exp(-(q-2*pi/c)**2*sigma**2/2)
    FonePeriod = ((exp(1j*q*tqw)-1)/(exp(1j*q*cqw)-1) + &
(exp(1j*q*tb)-1)/(exp(1j*q*cb)-1)*exp(1j*q*tqw))
    Fperiodic = (exp(1j*q*t*nperiods)-1)/(exp(1j*q*t)-1)
    Ffilm = exp(1j*q*tbuffer)*Fperiodic*FonePeriod*R
    Fbuffer = (exp(1j*q*tbuffer)*R-1)/(exp(1j*q*cb)-1)
    RS = log(abs(Ffilm + Fbuffer)**2)
plot(q,RS)
show()

It is, by the way, only natural to have an integer n, since crystals grow in discrete atomic layers, and not in arbitrarily small increments. Being a physicist, I should have seen that right away. What a shame.

Ahhhh, WTF. 😄

PS: Oh ja, the performance. With Fortran, you change the parameters, save, compile, and excute the program. Then you gnuplot the result. With Python, you change the parameters, save, and excute the program which plots the results. Well, what do you think?